Ap Physics Frq Satellite Of Mass M Orbits Earth Mechanical Energy

by

Feb 25, 2018  The mechanical energy of a satellite in circular orbit is solved for in terms of universal gravitational potential energy. And the velocity of the satellite. AP Physics Practice Test: Static Equilibrium, Gravitation, Periodic Motion ©2011, Richard White www.crashwhite.com! Calculate the period of the satellite. Calculate the satellite’s total mechanical energy at this altitude. Determine the escape velocity that was necessary for the satellite to be launched into this orbit from.

Orbits
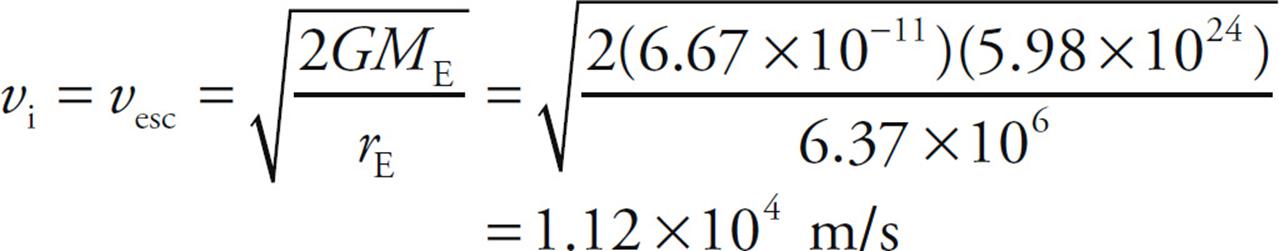
A satellite of mass m is in an elliptical orbit around the Earth, which has mass Me and radius Re. The orbit varies from closest approach of a at point A to maximum distance of b from the center of the Earth at point B. At point A, the speed of the satellite is vo.Express your answers in terms of a, b, m, Me, Re, vo, and G.
a. Write the expression for the gravitational force between the satellite and Earth at point b.
b. The potential energy of the satellite when it is a distance r from the center of the Earth is given by:
Ug=(-GMem)/r
Determine the total energy of the satellite when it is at A.
c. Determine the velocity of the satellite as it passes point B in its orbit.
As the satellite passes point A, a rocket engine on the satellite is fired so that its orbit is changed to a circular orbit of radius a about the center of the Earth.
d. determine the speed of the satellite for this circular orbit.
e. calculate the work done in changing the orbit
----------------------------
I honestly don't know where to start with this problem..any initial help would be very much appreciated :)

Unit 07: Rotation & Equilibrium

Chapter 8

Objectives:
Rigid bodies, translations and rotations
  • By the end of this unit of study, students should be able to (a) distinguish between pure translational and pure rotational motions of a rigid body and (b) state the conditions for rolling without slipping.
Torque, equilibrium and stability
  • By the end of this unit of study, students should be able to (a) define torque, (b) apply the conditions for mechanical equilibrium and (c) describe the relationship between the location of the center of gravity and stability.
  • Students should understand the concept of torque, so they can:
    • Calculate the magnitude and direction of the torque associated with a given force.
    • Calculate the torque on a rigid object due to gravity.
Rotational dynamics
  • By the end of this unit of study, students should be able to (a) describe the moment of inertia of a rigid body and (b) apply this rotational form of Newton's second law to physical situations.
Rotational work and kinetic energy
  • By the end of this unit of study, students should be able to discuss, explain and use the rotational forms of work, kinetic energy and power.
Angular momentum
  • By the end of this unit of study, students should be able to (a) define angular momentum and (b) apply the conservation of angular momentum to physical situations.

Students should be able to analyze problems in statics, so they can:
  1. State the conditions for translational and rotational equilibrium of a rigid object.
  2. Apply these conditions in analyzing the equilibrium of a rigid object under the combined influence of a number of coplanar forces applied at different locations.



Get voicey for mac.




A force exerted on an object can cause a torque on that object.
Quantities such as angular acceleration, velocity, and momentum are defined as vector quantities, but in this course the determination of “direction” is limited to clockwise and counterclockwise with respect to a given axis of rotation.
Only the force component perpendicular to the line connecting the axis of rotation and the point of application of the force results in a torque about that axis.
  1. The lever arm is the perpendicular distance from the axis of rotation or revolution to the line of application of the force.
  2. The magnitude of the torque is the product of the magnitude of the lever arm and the magnitude of the force.
  3. The net torque on a balanced system is zero.
Learning Objective (3.F.1.1):
The student is able to use representations of the relationship between force and torque.

The student is able to compare the torques on an object caused by various forces.

The student is able to estimate the torque on an object caused by various forces in comparison to other situations.

The student is able to design an experiment and analyze datatesting a question about torques in a balanced rigid system.

The student is able to calculate torques on a two-dimensional system in static equilibrium, by examining a representation or model (such as a diagram or physical construction).

Rotational motion
The presence of a net torque along any axis will cause a rigid system to change its rotational motion or an object to change its rotational motion about that axis.
  1. Rotational motion can be described in terms of angular displacement, angular velocity, and angular acceleration about a fixed axis.
  2. Rotational motion of a point can be related to linear motion of the point using the distance of the point from the axis of rotation.
  3. The angular acceleration of an object or rigid system can be calculated from the net torque and the rotational inertia of the object or rigid system.
Learning Objective (3.F.2.1):
The student is able to make predictions about the change in the angular velocity about an axis for an object when forces exerted on the object cause a torque about that axis.

The student is able to plan data collection and analysis strategiesdesigned to test the relationship between a torque exerted on an object and the change in angular velocity of that object about an axis.

angular momentum

A torque exerted on an object can change the angular momentum of an object.
  1. Angular momentum is a vector quantity, with its direction determined by a right-hand rule.
  2. The magnitude of angular momentum of a point object about an axis can be calculated by multiplying the perpendicular distance from the axis of rotation to the line of motion by the magnitude of linear momentum.
  3. The magnitude of angular momentum of an extended object can also be found by multiplying the rotational inertia by the angular velocity.
  4. The change in angular momentum of an object is given by the product of the average torque and the time the torque is exerted.
Learning Objective (3.F.3.1):
The student is able to predict the behavior of rotational collisionsituations by the same processes that are used to analyze linear collision situations using an analogy between impulse and change of linear momentum and angular impulse and change of angular momentum.

In an unfamiliar context or using representations beyond equations, the student is able to justify the selection of a mathematical routine to solve for the change in angular momentum of an object caused by torques exerted on the object.

The student is able to plan data collection and analysis strategiesdesigned to test the relationship between torques exerted on an object and the change in angular momentum of that object.


A net torque exerted on a system by other objects or systems will change the angular momentum of the system.
Torque, angular velocity, angular acceleration, and angular momentum are vectors and can be characterized as positive or negative depending upon whether they give rise to or correspond to counterclockwise or clockwise rotation with respect to an axis.
Learning Objective (4.D.1.1):
The student is able to describe a representation and use it to analyze a situation in which several forces exerted on a rotating system of rigidly connected objects change the angular velocity and angular momentum of the system.

The student is able to plan data collection strategies designed to establish that torque, angular velocity, angular acceleration, and angular momentum can be predicted accurately when the
variables are treated as being clockwise or counterclockwise with respect to a well-defined axis of rotation, and refine the research question based on the examination of data.
[See Science Practices 3.2, 4.1, 4.2, 5.1, and 5.3]


The angular momentum of a system may change due to interactions with other objects or systems.
  1. The angular momentum of a system with respect to an axis of rotation is the sum of the angular momenta, with respect to that axis, of the objects that make up the system.
  2. The angular momentum of an object about a fixed axis can be found by multiplying the momentum of the particle by the perpendicular distance from the axis to the line of motion of the object.
  3. Alternatively, the angular momentum of a system can be found from the product of the system’s rotational inertia and its angular velocity.
Learning Objective (4.D.2.1):
The student is able to describe a model of a rotational system and use that model to analyze a situation in which angular momentum changes due to interaction with other objects or systems.

The student is able to plan a data collection and analysis strategyto determine the change in angular momentum of a system and relate it to interactions with other objects and systems.



The change in angular momentumis given by the product of the average torque and the time interval during which the torque is exerted.
Learning Objective (4.D.3.1):
The student is able to use appropriate mathematical routines to calculate values for initial or final angular momentum, or change in angular momentum of a system, or average torque or
time during which the torque is exerted in analyzing a situation involving torque and angular momentum.

The student is able to plan a data collection strategy designed to test the relationship between the change in angular momentum of a system and the product of the average torque applied to the system and the time interval during which the torque is exerted.

Conservation of angular momentum
The angular momentum of a system is conserved.
If the net external torque exerted on the system is zero, the angular momentum of the system does not change.
Learning Objective (5.E.1.1):
The student is able to make qualitative predictions about the angular momentum of a system for a situation in which there is no net external torque.

The student is able to make calculations of quantities related to the angular momentum of a system when the net external torque on the system is zero.


The angular momentum of a system is determined by the locations and velocities of the objects that make up the system. The rotational inertia of an object or system depends upon the distribution of mass within the object or system. Changes in the radius of a system or in the distribution of mass within the system result in changes in the system’s rotational inertia, and hence in its angular velocity and linear speed for a given angular momentum. Examples should include elliptical orbits in an Earth-satellite system. Mathematical expressions for
the moments of inertia will be provided where needed. Students will not be expected to know the parallel axis theorem.
Learning Objective (5.E.2.1):
The student is able to describe or calculate the angular momentum and rotational inertia of a system in terms of the locations and velocities of objects that make up the system. Students are expected to do qualitative reasoning with compound objects. Students are expected to do calculations with a fixed set of extended objects and point masses.



Video (MIT) - Lecture 19: Rotating rigid bodies
Objectives:
Students should understand the concept of torque, so they can:
Calculate the magnitude and direction of the torque associated with a given force.
Calculate the torque on a rigid object due to gravity.
Students should be able to analyze problems in statics, so they can:
State the conditions for translational and rotational equilibrium of a rigid object.
Apply these conditions in analyzing the equilibrium of a rigid object under the combined influence of a number of coplanar forces applied at different locations.
Tutorial (Univ. of California) - Torque & rotational statics
Tutorial (Khan Academy) - Center of mass
Tutorial (Khan Academy) - Introduction to torque
Video (MIT) - Lecture 21: Torques
Video (MIT) - Lecture 25: Static equilibrium
Virtual lab (PhET) - Balancing act
Video (MIT) - Lecture 24: Rolling motion
*Book work: These are questions & problems from your text. This practice is to be completed along with any classwork and turned in on the day of the 'quiz/test'.
Conceptual (write and answer all questions)
  • Text
Exercises/problems (write the problems and show all work)
  • 52, 54, 65, 67, 68, 82, 87, 88, 98, 100 & *103
*All highlighted entries are to be turned in for a grade
Subpages (5):1: Torque2: Rotational dynamics3: Rotational Work4: Angular Momentum5: Mousetrap car challenge